An interesting calculator discovery and the result of a 12-hour drive

by David · Published March 12, 2021 · Updated March 13, 2022

I recently drove 12 hours from our home in Santa Fe to our beach spot in Mexico while Sonya had numerous virtual meetings and phone calls en route. This meant that I was not able to listen to music nor any of my podcasts as I do not like to drive with earphones in use. No matter, I had come across something interesting a few days prior and I spent most of the entire drive focused on it. I wrote a draft of this post in my notebook the next morning so I wouldn’t forget it.

A few days prior I was working on something and noticed the following. Suppose you started with the number 2 and then squared it. You get the number 4. Squared again, 8. Then 16, then 32, and so on. What I noticed was the last digit of each subsequent squaring, written down as {2, 4, 8, 6, 2}. After five such squares, that is after reaching $2^5$ , we end up back at 2. From there the cycle repeats. Here are the various powers of 2 and the last digit of each

Rendered by QuickLaTeX.com

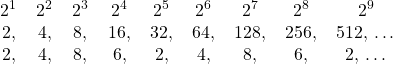
This is not unique to the number 2. Any number raised to increasing integer powers will show a cycle. What is interesting is that there will never be a cycle length larger than 5 when looking at the frequency of occurrence of the last digit. Shown in the next table are the various cycles that may appear.

Rendered by QuickLaTeX.com

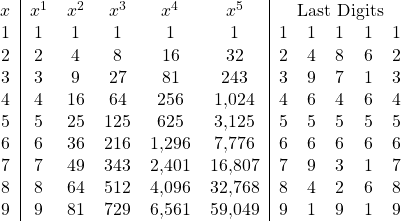
We see that not all cycles are of length 5. For 1, 5, and 6, in fact, the cycle length is only 1. The numbers 4 and 9 have cycles of length 2. But there is no cycle greater than length five. Why is that? And why is it that no matter what the starting number is, we will reach the same last digit after raising any number to a fifth power?

This applies to numbers of more than a single digit, of course. Suppose we started with the number 83. In successive powers we have 83, $\,$ 6,889, $\,$ 571,787, $\,$ 47,458,321, and 3,939,040,643. The cycle of last digits is {3, 9, 7, 1, 3}, the same as for the digit 3, itself. No matter how large of a number we start with, after raising it to successive powers the last digit will cycle back around to the last digit of the number with which we started, following one of the cycles appearing in the table above for single digits. If it is not clear why this is so, think about what a multiple digit number is. It is a single digit, plus another digit multiplied by 10, plus another digit multiplied by 100, and so on. Consider a two-digit number $10y + x$ where $x$ and $y$ are single digits. Squaring it gives

$\begin{equation*} (10y + x)^2 = 100y^2 + 20yx + x^2 \end{equation*}$

The first two terms on the right end in 0 so the last digit will be determined by the last digit of $x^2$ .

Thus the questions remain, why are there no cycles greater than 5 and why, no matter what, when we raise any number to the power of 5 do we get a number whose last digit is the same as the number with which we began?

When talking about cycles that appear in numbers there is a good chance that we will be making use of modular arithmetic, a part of mathematics based on wrap-around behavior. If you are unfamiliar with this subject, think of how most Americans keep time using a 12-hour clock. Let $n$ represent the number of hours that have passed since midnight. We would say that the current hour is $n$ mod 12, that is, it is the reminder after dividing by 12. If n = 6 then 12 goes into 6 zero times, with a remainder of 6. So it is 6 AM. If n = 14 then 12 goes into 14 once with a remainder of 2. It’s 2 PM. We say the hour of the day is based on a modular-12 system.

Modular arithmetic will come into play in our explanation for the questions raised at the end of the last section. We will use the concept of congruence between numbers based on some modular value. Two values $a$ and $b$ are said to be congruent based on some modular value $m$ if the difference between the two values is evenly divisible by $m$ . This is written as

$a \equiv b \pmod{m}.$

Note the three-lined equivalence symbol being used and the ‘(mod m)’. The parentheses around the latter indicate that it applies to the whole equation, both the left and right sides. The notation is not too complicated and means nothing more than the difference $a-b$ is evenly divisible by $m$ , i.e. $a-b = km$ for some integer $k$ . Another way mathematicians write “is evenly divisible by” is the following notation,

$m|(a-b) .$

Keep in mind the ‘(mod m)’ type of notation in what follows. A common temptation is to think that the statement $a \equiv b \pmod{m}$ is a shorthand way to say, “ $b$ is the remainder when $a$ is divided by $m$ .” However, this is not always the case. Here are a few examples to drive home the meaning of the congruence relation.

$12 \equiv 8 \pmod{4},$

because $12-8=4$ is evenly divisible by 4. Note that $8$ is definitely not the remainder of $12 \div 4$ .

$33 \equiv 1 \pmod{16},$

because $33-1=32$ is evenly divisible by 16.

An interesting theorem involving modular arithmetic and prime numbers was introduced by Fermat and is known as Fermat’s Little Theorem in deference to his more famous Last Theorem.

Recall that a prime number is one that is only divisible by itself and the number 1. Fermat’s Little Theorem states that for any prime number $p$ and any number $a$ not divisible by $p$ that

$a^{p-1} \equiv 1 \pmod{p}.$

This theorem is essential to answering our questions so it is worth showing a proof. Also, it leads to a generalization due to Euler that will more directly answer our questions.

To prove Fermat’s Little Theorem, start by creating a set of numbers from 1 to $p-1$ . Call this set $S$ ,

$S = \{ 1, 2, 3, \ldots p-1\}.$

There are a total of $p-1$ elements of $S$ , all less than $p$ , and so it should be obvious that for any member $n$ of $S$ , written as $n \in S$ , that $n$ mod $p$ = $n$ . So every member of $S$ is unique and every member has a unique congruence modulo $p$ , that is, a unique remainder mod $p$ , namely itself. Next form a new set $a \cdot S$ where we multiply every member of $S$ by $a$ . This new set is

$a \cdot S = \{ a, 2a, 3a, \ldots (p-1)a \}.$

Every element of this new set also has a unique congruence modulo $p$ . To show this, assume that two members of $a\cdot S$ had the same congruence relationship modulo $p$ . That is,

$na \equiv ma \equiv q \pmod{p}$

for some integer q. This implies that $na = kp + q$ and $ma = k^{'}p + q$ for integers $k, k^{'}$ . If we subtract these we get

$na - ma = (k-k^{'})p.$

The right-hand side is clearly divisible by p and this means that

$(n-m) a \equiv 0 \pmod{p}.$

The integers $n$ and $m$ are both less than $p$ because of how the set $S$ was constructed, hence their difference must also be less than $p$ . This fact, combined with the assertion at the beginning that $a$ is not divisible by $p$ , means that the only way the above congruence relation can hold true is if $n = m$ , proving the congruence uniqueness for the set $a \cdot S$ .

We have just shown that all of the congruences of the set $a\cdot S$ are unique. Each one is also less than $p$ by definition of taking the modulus with $p$ , so there is a one-to-one correspondence with the congruences of the set $S$ with those of the set $a\cdot S$ . The congruences modulo $p$ of the set $a \cdot S$ are a permutation of those of $S$ . However, we can multiply all these congruences to see that

$1\cdot 2\cdot3\cdots (p-1) \equiv a\cdot 2a \cdot 3a \cdots (p-1)a \pmod{p},$

$(p-1)! \equiv (p-1)! \, a^{p-1} \pmod{p},$

and finally, we can divide each side by $(p-1)!$ to get the result, Fermat’s Little Theorem,

$a^{p-1} \equiv 1 \pmod{p}.$

Euler extended Fermat’s Little Theorem to non-prime values of $p$ . Suppose $m$ is any integer and that $a$ and $m$ are coprime. This just means that the greatest common divisor of either number is 1, written gcd( $a,m$ ) = 1. Then in general Fermat’s Little Theorem does not hold. We already see a problem with the set $S = \{1, 2, 3, \ldots (m-1)\}$ . Some of those elements may have the same congruence relations modulo $m$ . Instead, we form a new set containing only the numbers 1 to $m-1$ that are coprime to $m$ . For example, if $m=12$ our set would look like this,

$S = \{ 1,5,7,11\}.$

Those are the only numbers in the range 1 to 12 that are coprime to 12. (Numbers are not considered coprime to themselves.) The number of elements of $S$ is denoted $\phi(m)$ and is called Euler’s totient function. $\phi(m)$ is the count of numbers less than $m$ that are coprime to $m$ . There is no general function to write down in order to compute $\phi(m)$ but it has been tabulated for numerous values in various tables. Here we show just a few examples.

$\begin{eqnarray*} m & \phi(m) & S\{m\} \\ 2 & 1 & \{1\} \\ 3 & 2 & \{1, 2\} \\ 4 & 2 & \{ 1,3\} \\ 5 & 4 & \{ 1,2,3,4 \} \\ 6 & 2 & \{1, 5\} \\ 10 & 4 & \{1, 3, 7, 9 \} \\ 15 & 8 & \{1, 2, 4, 7, 8, 11, 13, 14\} \\ 17 & 16 & \{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17\} \end{eqnarray*}$

Note in particular the last row. For any prime number $p$ we have $\phi(p) = p-1$ and you should see that Fermat’s Little Theorem is just a special case of Euler’s Theorem when $m$ is a prime number. Another property of the totient function is that for any two prime numbers $p$ and $q$ , $\phi(pq) = \phi(p) \phi(q)$ .

Let’s return to the new set $S = \{n_1, n_2, n_3, \ldots, n_{\phi(m)} \}$ . As for the case in proving Fermat’s Little Theorem, each of these numbers $n_i$ is less than $m$ and the congruences are all unique. Again we form a new set $a\cdot S$ where we multiply each member of $S$ by the number $a$ .

$a \cdot S = \{an_1, an_2, an_3, \ldots, an_{\phi(m)} \}.$

If $a n_i \equiv k \pmod{m}$ and $a n_j \equiv k \pmod{m}$ for some $i, j$ then this implies that $m$ divides $(n_i - n_j) a$ , but $a$ and $m$ are coprime so we know $m$ does not divide $a$ . Thus $m$ can only divide $n_i - n_j$ which can only happen if $i=j$ . Therefore, the set $a\cdot S$ is a permutation of all the congruences contained in $S$ modulo $m$ , just as what we found for the sets used to prove Fermat’s Little Theorem. As before, we now multiply all the congruences to see that

$(n_1 \cdot n_2 \cdot n_3 \cdots n_{\phi(m)}) \equiv (n_1a \cdot n_2a \cdot n_3a \cdots n_{\phi(m)}a) \pmod{m},$

$(n_1 \cdot n_2 \cdot n_3 \cdots n_{\phi(m)}) \equiv (n_1 \cdot n_2 \cdot n_3 \cdots n_{\phi(m)}) a^{\phi(m)} \pmod{m},$

and upon dividing each side by the $n_i$ multiplication terms, we arrive at Euler’s Theorem for numbers $a$ and $m$ coprime,

$a^{\phi(m)} \equiv 1 \pmod{m}.$

As a corollary we can multiply both sides by $a$ to get the relationship

$a^{\phi(m)+1} \equiv a \pmod{m}.$

So how does Euler’s Theorem help answer the question of why there is no cycle length greater than 5 for examining the last digit when raising numbers to successive powers? We’re getting there.

Suppose $m=\alpha \beta$ where both $\alpha$ and $\beta$ are prime numbers and neither one divides $a$ . Then we will claim that

$a^{\phi(\alpha \beta)+1} = a \pmod{\alpha\beta}$

holds for all values of $a$ , not just those coprime to $\alpha\beta$ .

If $a = \alpha\beta$ then it is obviously true. If $a$ is not a multiple of either $\alpha$ or $\beta$ then it is true by Euler’s Theorem. All that is left is to consider the case where $a$ is a multiple of either $\alpha$ or $\beta$ . Suppose $a = k\alpha$ for some integer $k$ . Then

$(k\alpha)^{\phi(\alpha\beta) + 1} \equiv k\alpha \pmod{\alpha\beta}$

means that

$\alpha\beta \left| \left[ (k\alpha)^{\phi(\alpha\beta) + 1} - k\alpha \right] \right.,$

i.e. that $\alpha\beta$ divides the terms in brackets. We can clearly divide $k\alpha$ from both terms in the brackets so all that is left is to show the $\beta$ divides the terms

$(k\alpha)^{\phi(\alpha\beta) } - 1$

Note that that by our assumptions ( $\alpha$ and $\beta$ both prime numbers) that $\gcd{(k,\alpha)} = 1$ , and $\gcd{(\alpha, \beta)} = 1$ . By Euler’s Theorem we have that

$\beta \left| \left[ (k\alpha)^{\phi(\beta)} - 1 \right] \right.$

$(k\alpha)^{\phi(\beta)} \equiv 1 \pmod{\beta}.$

By the multiplicative property of modular arithmetic (see appendix) we can raise the power of $(k\alpha)^{\phi(\beta)}$ and the congruence relation will still hold, so

$\left[ (k\alpha)^{\phi(\beta)}\right]^{\phi(\alpha)} = (k\alpha)^{\phi(\beta)\phi(\alpha)} = (k\alpha)^{\phi(\alpha\beta)} \equiv 1 \pmod{\beta},$

where we made use of the fact that $\phi(\alpha\beta) = \phi(\alpha)\phi(\beta)$ for prime numbers.

To restate, for any number $a$ and $m=\alpha\beta$ where $\alpha$ and $\beta$ are both prime,

$a^{\phi(m)} \equiv 1 \pmod{m}.$

Finally, to address our questions let $\alpha=2$ and $\beta = 5$ , so that $m=10$ . We know that $\phi(10) = 4$ from the previous chart. By Euler’s Theorem then, for any number $a$ ,

$a^4 \equiv 1 \pmod{10},$

and

$a^5 \equiv a \pmod{10}.$

The fact that $a^5 - a$ is evenly divisible by 10 means that any number that has been raised to the fifth power ends in a digit that is the same as the last digit of $a$ , answering one of our questions. We also know from earlier discussions that once a number ends in the same digit as the last digit of the number with which we began, that the cycle starts again. There can be no cycle of length greater than 5.